Matemáticas 1º Bachillerato Humanidades y Ciencias Sociales
lunes, 27 de mayo de 2019
ESTÁNDARES MÍNIMOS PARA LA CONVOCATORIA EXTRAORDINARIA DE MATEMÁTICAS SEPTIEMBRE 2019
Hola, os pongo un enlace con los estándares a evaluar en matemáticas aplicadas a las ciencias sociales I, en la convocatoria de septiembre de 2019. Pinchad en el siguiente enlace: ESTÁNDARES MÍNIMOS SEPTIEMBRE 2019
miércoles, 26 de septiembre de 2018
practicando potencias y raíces en la parada de autobús
Hola, os dejo una entrada a una página con ejercicios interactivos para practicar potencias y raíces. Podéis elegir el tipo de ejercicio y el nivel.
Potencias, raíces y otros
Potencias, raíces y otros
miércoles, 19 de septiembre de 2018
jueves, 11 de mayo de 2017
ÚLTIMO TEMA: LA DISTRIBUCIÓN DE PROBABILIDAD CONTINUA, LA DISTRIBUCIÓN NORMAL N( 0, 1)
Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa por N(μ, σ), si se cumplen las siguientes condiciones:

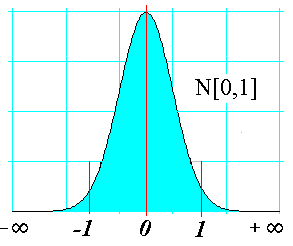

1. La variable puede tomar cualquier valor: (-∞, +∞)
2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:

Esta función, de difícil expresión algebraica,
tiene una gráfica característica, llamada comúnmente
CAMPANA DE GAUSS y tiene las siguientes características:
tiene una gráfica característica, llamada comúnmente
CAMPANA DE GAUSS y tiene las siguientes características:
El campo de existencia es cualquier valor real, es decir, (-∞, +∞).
Es simétrica respecto a la media µ.
Tiene un máximo en la media µ.
Crece hasta la media µ y decrece a partir de ella.
En los puntos µ − σ y µ + σ presenta puntos de inflexión.
El eje de abscisas es una asíntota de la curva.
El área del recinto determinado por la función y el eje de abscisas es igual a la unidad.
Como toda distribución de probabilidad continua, NO PERMITE CALCULAR probabilidades de valores concretos, sino la probabilidad de intervalos entre dos valores cualquiera de la variable.
Por suerte, el cálculo de probabilidades es fácil y accesible ya que está tabulada. Es decir, las probabilidades se calculan a partir de una tabla de valores de una distribución de media 0 y de desviación típica 1. También se llama N(0, 1).

La tabla mide la probabilidad desde -∞ hasta un valor k, es decir mide p(z≤ k), que es la tabla que tenéis en el cuadernillo. Con esta tabla y conociendo las propiedades de la probabilidad podemos calcular cualquier caso

p(z =a) = 0
p(z≤ a) = f(a) ---> se mira directamente en la tabla
p(a < z ≤ b) = f(b) - f(a)
p(z> a) = 1 - p(z≤ a) = 1 - f(a)
Esta tabla tiene además el inconveniente de que no puedes encontrar probabilidades para valores de z negativos, pero al ser una función simétrica podemos hacer los cálculos de la siguiente manera
p(z≤ -a) = p(z> a) = 1 - p(z≤ a) = 1 - f(a)
p(z> -a) = p(z≤ a) = f(a)
Os pongo el enlace a una página para practicar, AQUÍ
miércoles, 10 de mayo de 2017
REPASOS DE PROBABILIDAD Y DISTRIBUCIÓN BINOMIAL
Hola, os pongo los enlaces a páginas web con ejercicios de probabilidad para practicar en casa y para repasar. Todos los ejercicios tienen su solución.
Repaso de probabilidad
Ejercicios de probabilidad (pdf a partir de página 438)
Repaso de distribución binomial (pdf a partir de página 474)
Recordad que en el examen no voy a poner ejercicios complicados
Repaso de probabilidad
Ejercicios de probabilidad (pdf a partir de página 438)
Repaso de distribución binomial (pdf a partir de página 474)
Recordad que en el examen no voy a poner ejercicios complicados
martes, 25 de abril de 2017
DISTRIBUCIÓN DE PROBABILIDAD DISCRETA: DISTRIBUCIÓN BINOMIAL

Hola, hoy hemos empezado el penúltimo tema del curso. La distribución binomial. Esta se caracteriza por una serie n de experimentos independientes, que puede tomar dos posibilidades:
Éxito: con una probabilidad constante p
Fracaso: con una probabilidad también constante (1 -p) también llamada q
El cálculo de probabilidades de x éxitos y por tanto (n -x) fracasos independientemente del orden en que se produzcan los éxitos o fracasos se puede calcular con la siguiente fórmula o función

Dicho esto, cuando un experimento aleatorio sigue una distribución binomial, lo abreviamos con los datos siguientes B(n, p)
El cálculo de los parámetros representativos se calcula muy fácilmente a partir de lo escrito anteriormente.
Media = n·p
Desviación típica = raíz cuadrada de n·p·(1-p)
Os dejo con un enlace a problemas típicos de distribución binomial AQUÍ
jueves, 20 de abril de 2017
CÁLCULO DE PROBABILIDADES A POSTERIORI. TEOREMA DE BAYES
Hola, os pongo un vídeo con un ejercicio resuelto paso a paso para cálculo de probabilidades a posteriori. La distinción entre cálculo de probabilidades a priori y a posteriori, es que mientras a priori calculamos las probabilidades sabiendo las condiciones de antemano, en las probabilidades a posteriori es que conociendo el resultado final de lo que ha ocurrido podamos calcular la probabilidad de que se haya originado al principio de una manera u otras.
Como dicen en el video no hace falta saber aplicar el teorema de Bayes, pues su formulación es muy complicada, sino saber aplicar una probabilidad condicionada. También se puede resolver con una tabla de contingencia como veréis aquí abajo si os traduzco el ejemplo a una tabla
Nos quedamos con la fila de la condición que se ha cumplido, es decir, que ha sucedido bola roja, y dividimos la casilla de la urna 1 con el total de sacar roja.
Como dicen en el video no hace falta saber aplicar el teorema de Bayes, pues su formulación es muy complicada, sino saber aplicar una probabilidad condicionada. También se puede resolver con una tabla de contingencia como veréis aquí abajo si os traduzco el ejemplo a una tabla
Urna 1
|
Urna 2
|
Total
|
|
Roja
|
½ · 2/6= 1/6
|
½ · 3/5= 3/10
|
7/15
|
Amarilla
|
½ · 4/6=2/6
|
½ · 2/5= 1/5
|
8/15
|
Total
|
1/2
|
1/2
|
1
|
P(urna1 / R) = 1/6 : 7/15 = 5/14
Suscribirse a:
Entradas (Atom)